两周前有同学在qq群中讨论PLL的参数设计,之前没自己动手计算过,一直用的将PLL传递函数,忽略零点项,当做标准的二阶系统近似处理,类似ζ=0.707,wn=wc的近似吧。我搜过一些文章也都是这样写的,其实它的频率响应表现还是不太一样的。
电机控制qq群:528884293
传递函数和频率响应:
PLL框图:

G ( s ) = K p s + K i s 2 G(s)=\frac{K_ps+K_i}{s^2}G(s)=s2Kps+Ki
G ( s ) c l o s e = K p s + K i s 2 1 + K p s + K i s 2 G(s)_{close}=\frac{\frac{K_ps+K_i}{s^2} }{1+\frac{K_ps+K_i}{s^2}}G(s)close=1+s2Kps+Kis2Kps+Ki
G ( s ) c l o s e = K p s + K i s 2 + K p s + K i G(s)_{close}=\frac{K_ps+K_i} {s^2+K_ps+K_i}G(s)close=s2+Kps+KiKps+Ki
其中:
K p = 2 ζ ω n K_p = 2\zeta \omega_nKp=2ζωn
K i = ω n 2 K_i = \omega_n^2Ki=ωn2
得到
G ( s ) C L = 2 ζ ω n s + ω n 2 s 2 + 2 ζ ω n s + ω n 2 G(s)_{CL}=\frac{2\zeta \omega_n s+\omega^2_n} {s^2+2\zeta \omega_ns+\omega^2_n}G(s)CL=s2+2ζωns+ωn22ζωns+ωn2
设
ω ω n = Ω \frac{\omega}{\omega_n} =\Omegaωnω=Ω
G ( s ) C L = 2 ζ ω ω n j + 1 − ω 2 ω n 2 + 2 ζ ω ω n j + 1 G(s)_{CL}=\frac{2\zeta \frac{ \omega }{ \omega_n}j+1} {-\frac{\omega^2}{\omega_n^2} +2\zeta \frac{ \omega }{ \omega_n} j +1}G(s)CL=−ωn2ω2+2ζωnωj+12ζωnωj+1
= 2 ζ Ω j + 1 − Ω 2 + 2 ζ Ω j + 1 =\frac{2\zeta \Omega j +1} {-\Omega^2 +2\zeta \Omega j +1}=−Ω2+2ζΩj+12ζΩj+1
= ( 1 − Ω 2 − 2 ζ Ω j ) ( 2 ζ Ω j + 1 ) ( 1 − Ω 2 + 2 ζ Ω j ) ( 1 − Ω 2 − 2 ζ Ω j ) =\frac{(1-\Omega^2 - 2\zeta \Omega j)(2 \zeta \Omega j + 1)} {( 1-\Omega^2+2\zeta \Omega j ) (1- \Omega^2-2\zeta \Omega j)}=(1−Ω2+2ζΩj)(1−Ω2−2ζΩj)(1−Ω2−2ζΩj)(2ζΩj+1)
= 1 − Ω 2 + 4 ζ 2 Ω 2 ( 1 − Ω 2 ) 2 + 4 ζ 2 Ω 2 − 2 ζ Ω 3 ( 1 − Ω 2 ) 2 + 4 ζ 2 Ω 2 j =\frac{1-\Omega^2+4\zeta^2 \Omega^2 } {( 1-\Omega^2)^2+4\zeta^2 \Omega^2 }- \frac{2\zeta \Omega^3}{(1- \Omega^2)^2 + 4 \zeta^2 \Omega^2}j=(1−Ω2)2+4ζ2Ω21−Ω2+4ζ2Ω2−(1−Ω2)2+4ζ2Ω22ζΩ3j
振幅响应:
∣ G ( j ω ) ∣ = ( R e a l ( G ( j ω ) ) 2 + I m ( G ( j ω ) ) 2 ) 1 2 |G(j\omega)|=(Real(G_{(j\omega)})^2 +Im(G_{(j \omega)})^2)^{\frac{1}{2}}∣G(jω)∣=(Real(G(jω))2+Im(G(jω))2)21
= ( 1 − Ω 2 + 4 ζ 2 Ω 2 ) 2 + ( 2 ζ Ω 3 ) 2 ( ( 1 − Ω 2 ) 2 + 4 ζ 2 Ω 2 ) 2 =\sqrt{\frac{(1-\Omega^2+4\zeta^2 \Omega^2)^2 + (2\zeta \Omega^3)^2} {(( 1-\Omega^2)^2+4\zeta^2 \Omega^2)^2 }}=((1−Ω2)2+4ζ2Ω2)2(1−Ω2+4ζ2Ω2)2+(2ζΩ3)2
假设 Ω = 1 \Omega = 1Ω=1 ,即ω = ω n \omega =\omega_nω=ωn的情况
∣ G ( j ω ) ∣ = 4 ζ 2 + 1 4 ζ 2 |G_{(j\omega)}|= \sqrt{\frac{4\zeta^2+1}{4\zeta^2}}∣G(jω)∣=4ζ24ζ2+1
ζ → ∞ , ∣ G ( j ω ) ∣ → 1 \zeta \rightarrow \infty , |G_{(j\omega)}| \rightarrow 1ζ→∞,∣G(jω)∣→1
可见ζ \zetaζ 的取值,无法像标准的二阶系统取ζ = 0.707 \zeta = 0.707ζ=0.707能让∣ G ( j ω ) ∣ = 2 2 |G_{(j\omega)}| = \frac{\sqrt{2}}{2}∣G(jω)∣=22,截止频率近似ω c = ω n \omega_c = \omega_nωc=ωn
使用matlab工具,固定ω n , ζ \omega_n ,\zetaωn,ζ 取几个不同的值,看伯德图
zeta = [0.1,0.5,0.707,1,5,10];
wn = 300;
figure(1);
for n=1:6
sys = tf([2*zeta(n)*wn,wn*wn],[1, 2*zeta(n)*wn,wn*wn]);
bode(sys);
hold on;
end
legend('ζ=0.1','ζ=0.5','ζ=0.707','ζ=1','ζ=5','ζ=10');1234567891011121314


固定了ω n \omega_nωn,看不同ζ \zetaζ的取值,频率响应的变化
-
ζ \zetaζ 取值越大,bode图的表现就更像一阶低通
-
ζ \zetaζ 取小,则会有更大的振幅响应
matlab工具,固定ζ , ω n \zeta,\omega_nζ,ωn取几个不同的值,看看伯德图
ζ = 0.707 , ω n \zeta =0.707,\omega_nζ=0.707,ωn 取不同值的情况


ζ = 1 , ω n \zeta =1,\omega_nζ=1,ωn 取不同值的情况

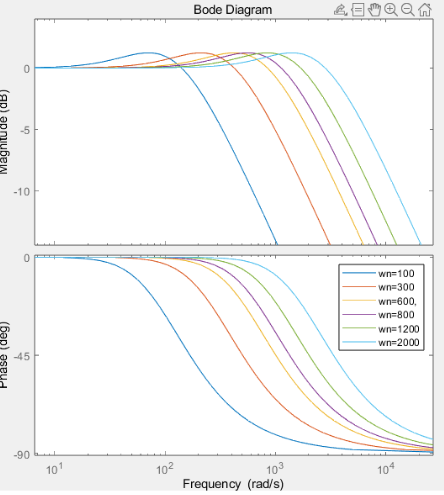
ζ = 5 , ω n \zeta =5,\omega_nζ=5,ωn 取不同值的情况

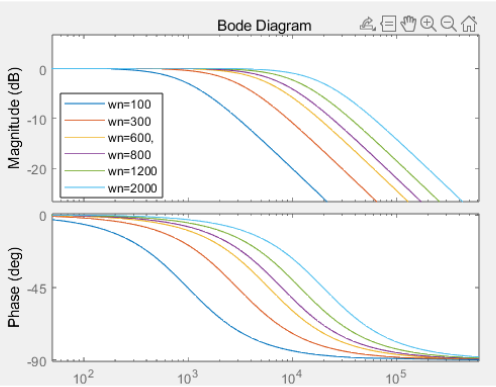 固定了ζ \zetaζ,不同的ω n \omega_nωn频率响应
固定了ζ \zetaζ,不同的ω n \omega_nωn频率响应
- ζ \zetaζ 阻尼决定了振幅。
- ω n \omega_nωn 决定了带宽,响应。
参数设计
对于一般数字滤波器的设计,我们的输入一般就是截止频率,或者比如像带通频率,带阻频率参数等等
标准的二阶系统取ζ = 0.707 \zeta = 0.707ζ=0.707能让∣ G ( j ω ) ∣ = 2 2 |G_{(j\omega)}| = \frac{\sqrt{2}}{2}∣G(jω)∣=22,使得近似截止频率ω c = ω n \omega_c = \omega_nωc=ωn
在这里对于PLL,ζ = 0.707 \zeta=0.707ζ=0.707也不是一个好的值,振幅峰值差不多有2db。
对于PLL的二阶系统我们如何设计K p , K i K_p,K_iKp,Ki呢,或者说如何选取ζ , ω n \zeta ,\omega_nζ,ωn
因为K p = 2 ζ ω n K_p = 2\zeta \omega_nKp=2ζωn,K i = ω n 2 K_i = \omega_n^2Ki=ωn2。选取ζ , ω n \zeta ,\omega_nζ,ωn,即得到了K p K_pKp和K i K_iKi
①首先要确定ζ \zetaζ,如果按照最小谐振峰值的要求,那ζ \zetaζ可以选择大一些。
- 这里选取两个值讨论 ζ = 1 , 10 \zeta= 1,10ζ=1,10
②我们希望设置一个截止频率ω c \omega_cωc,就需要知道ω n \omega_nωn和ω c \omega_cωc的关系
其实在matlab的伯德图中,其实也可以找出关系
当 ζ = 1 , ω c ≈ 2.5 ω n 当 \zeta= 1, \omega_c \approx 2.5\omega_n当ζ=1,ωc≈2.5ωn
当 ζ = 10 , ω c ≈ 20 ω n 当 \zeta= 10, \omega_c \approx 20\omega_n当ζ=10,ωc≈20ωn
理论计算:
∣ G ( j ω ) ∣ = ( 1 − Ω 2 + 4 ζ 2 Ω 2 ) 2 + ( 2 ζ Ω 3 ) 2 ( ( 1 − Ω 2 ) 2 + 4 ζ 2 Ω 2 ) 2 |G_{(j\omega)}|=\sqrt{\frac{(1-\Omega^2+4\zeta^2 \Omega^2)^2+ (2\zeta \Omega^3)^2} {(( 1-\Omega^2)^2+4\zeta^2 \Omega^2)^2 }}∣G(jω)∣=((1−Ω2)2+4ζ2Ω2)2(1−Ω2+4ζ2Ω2)2+(2ζΩ3)2
令 ∣ G ( j ω ) ∣ = 2 2 , ζ = 1 , 求 Ω 令|G_{(j\omega)}|=\frac{\sqrt{2}}{2}, \zeta = 1, 求\Omega令∣G(jω)∣=22,ζ=1,求Ω
( 1 − Ω 2 + 4 ζ 2 Ω 2 ) 2 + ( 2 ζ Ω 3 ) 2 ( ( 1 − Ω 2 ) 2 + 4 ζ 2 Ω 2 ) 2 = 2 2 \sqrt{\frac{(1-\Omega^2+4\zeta^2 \Omega^2)^2+ (2\zeta \Omega^3)^2} {(( 1-\Omega^2)^2+4\zeta^2 \Omega^2)^2 }} = \frac{\sqrt{2}}{2}((1−Ω2)2+4ζ2Ω2)2(1−Ω2+4ζ2Ω2)2+(2ζΩ3)2=22
Ω 8 − 4 Ω 6 − 12 Ω 4 − 8 Ω 2 − 1 = 0 \Omega^8-4\Omega^6-12\Omega^4-8\Omega^2-1=0Ω8−4Ω6−12Ω4−8Ω2−1=0
其中一个解 Ω = 10 + 3 ≈ 2.482 其中一个解\Omega=\sqrt{\sqrt{10}+3} \approx 2.482其中一个解Ω=10+3≈2.482
同理当ζ = 10 \zeta = 10ζ=10, 求Ω \OmegaΩ
其中一个解
Ω = 40402 + 201 ≈ 20.05 \Omega=\sqrt{\sqrt{40402}+201} \approx 20.05Ω=40402+201≈20.05
即:当选取ζ = 1 \zeta= 1ζ=1, 截止频率选1000时,ω n = 400 \omega_n=400ωn=400
K p = 2 ζ ω n = 800 K_p = 2\zeta \omega_n = 800Kp=2ζωn=800
K i = ω n 2 = 160000 K_i = \omega_n^2=160000Ki=ωn2=160000





评论(0)
您还未登录,请登录后发表或查看评论